LeetCode-hot100-medium #

介绍 #

一句话总结算法思路，LeetCode hot100 medium

按频率排序，排序依据参考 字节跳动后端高频面试题目。

全部源码可见我的GitHub interview-leetcode

注：

有下划线标志的都是超链接。 点击下列题目标题可以跳转到LeetCode中文官网直接阅读题目，提交代码。 点击下列代码链接，可以直接跳转到我的GitHub代码页面。每道题一般精选一种解法，我的GitHub中可能收录多种解法代码，请自行查看。

3.无重复字符的最长子串 #

题目： 在字符串中找一个子串，要求连续无重复字符且最长，只需要返回最大长度

题解：

• 字符串长度为0直接返回
• 记录最大子串的长度，用来和新子串长度比较，维护子串的状态还需要记录当前子串的起始位置的下标
• 使用map来储存字符对应的下标，
• 只要当前字符出现在map里，同时map里的字符就是子串里的字符时（存储的字符下标大于等于起始位置下标）说明重复，更新子串起始位置为map中记录的重复点+1
• else (没有出现在子串里)，子串长度++，判断更新最大长度(注意更新时+1)

代码： golang

215.数组中的第k个最大元素 #

题目： 数组中的第k个最大元素，比如第二大，就是找次大。

题解： 方法1，堆排序（不推荐）

• 求第K大的数，实际上就是取小根堆的根节点
• 小根堆的性质，根节点比所有叶子节点更小

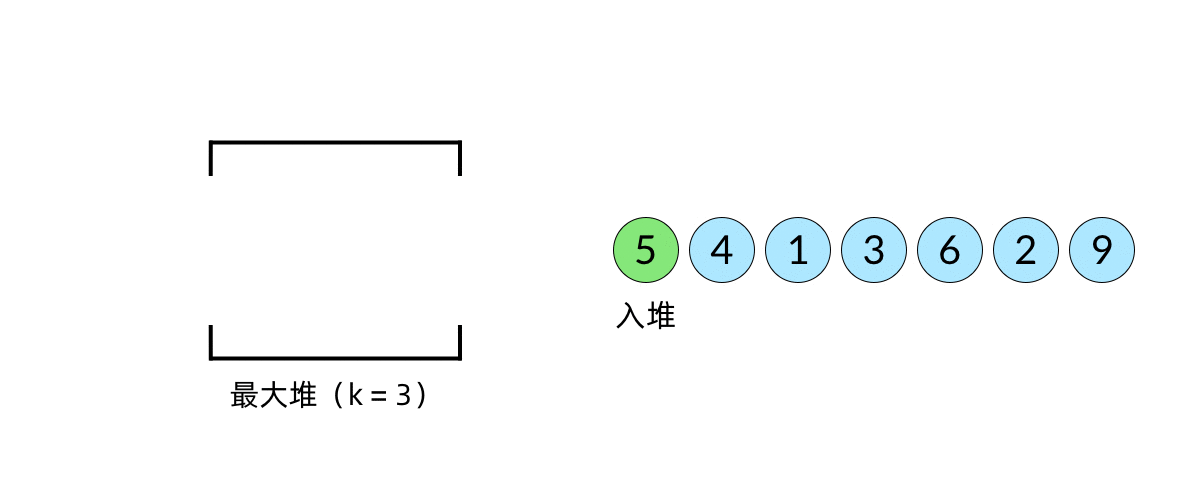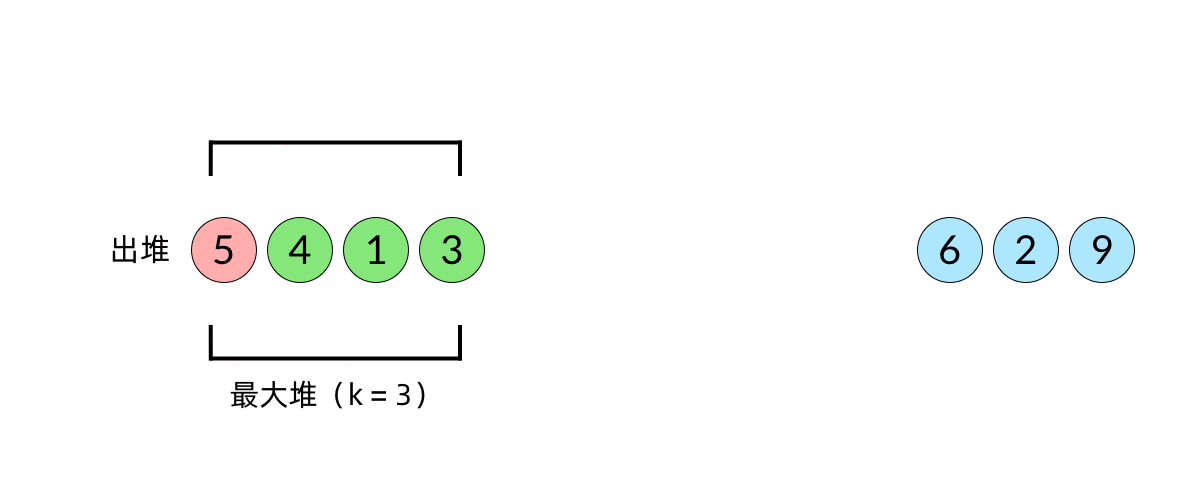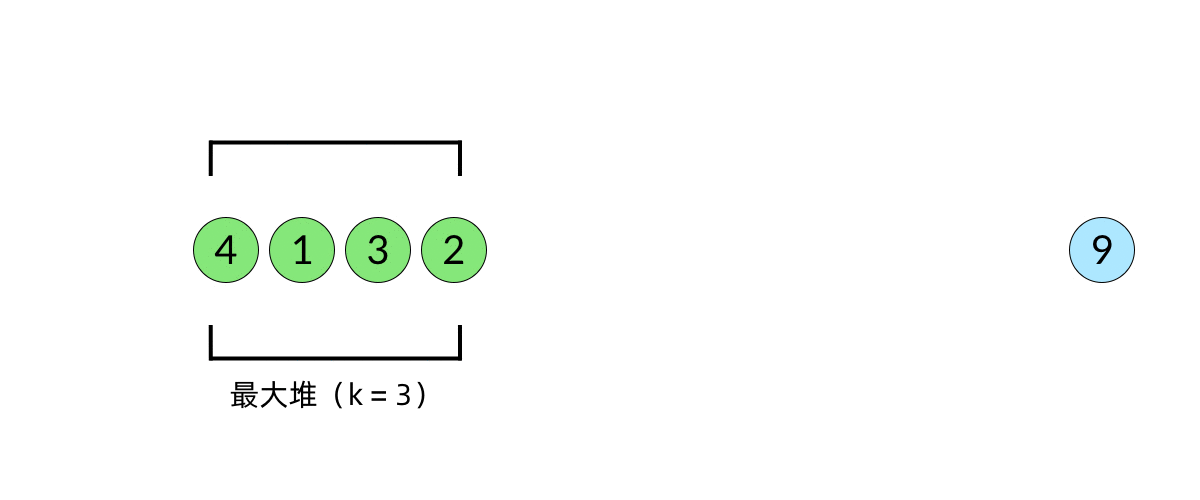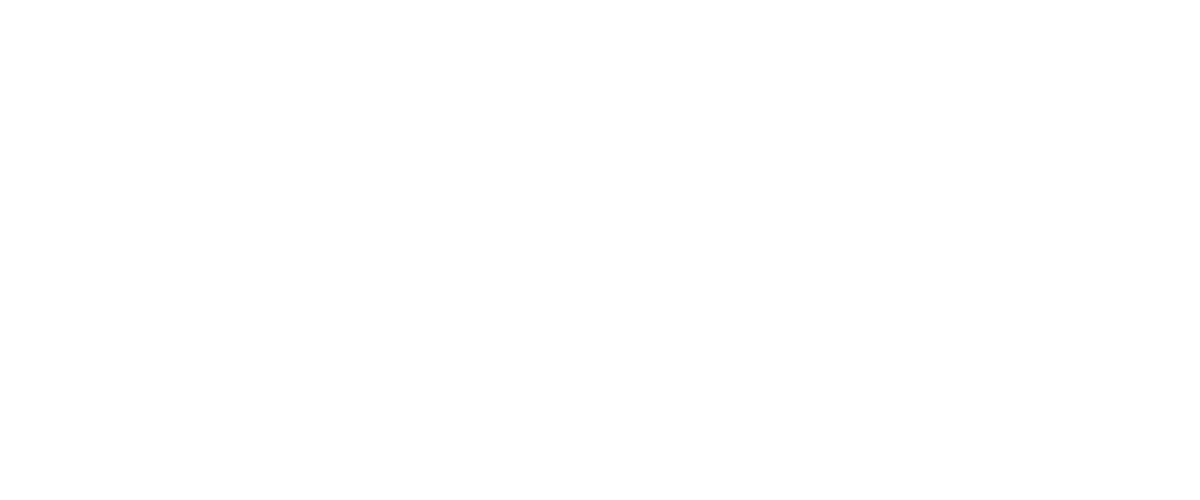
注意：这里为什么用堆，是因为堆是一个完全二叉树，而二叉搜索树不自平衡，而且堆的话小根堆保证堆个数为k，直接取根节点就是结果了

堆排序的好处是，假设k比较小，而数组比较大，不需要加载全部内容到内存里

方法2 快速排序变形（快速选择算法）

• 其实就是快排的思路，只是做了下剪枝
• 只要保证len-k这个位置右侧全部比k大，左侧全部小于等于k，那么len-k位置的数就是第k大

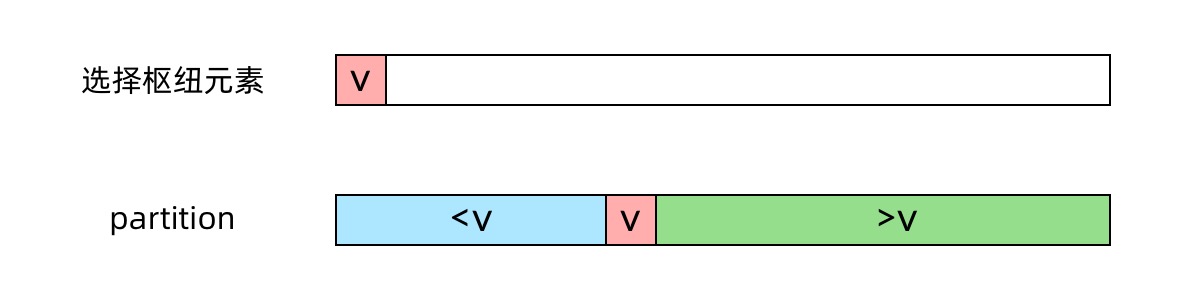
• 因为我们不知道是哪个数，所以随便取一个数x，最终达到左侧全部<=x，右侧全部>x的效果，核心代码如下

// 快排剪枝
func quickSelect(a []int, l, r, index int) int {
    // 查找中枢
    q := randomPartition(a, l, r)
    if q == index {
        return a[q]
    } else if q < index {
        return quickSelect(a, q + 1, r, index)
    }
    return quickSelect(a, l, q - 1, index)
}

• 把x的下标index和len-k比较，如果小，说明第k大数一定在[index+1,r]；如果大说明第k大数一定在[l,index-1]中
• 缩小区间，继续随便取一个数，直到正好x的下标就是len-k为止

查找中枢的办法借助快排的思路

//随机中枢
func randomPartition(a []int, l, r int) int {
    i := rand.Int() % (r - l + 1) + l
	// 因为把r的位置作为中枢，所以要交换
    a[i], a[r] = a[r], a[i]
    return partition(a, l, r)
}

• 随机取一个数x，把他和r位置的数对调
• 找到中枢的正确位置，保证左侧都比它小，右侧都比他大

//快排核心代码
func partition(a []int, l, r int) int {
	// 因为传入的中枢是r位置
    x := a[r]
	// 先把i设置为l-1区间之外，保证每次更新先++再更新
	// i 的作用是记录小于中枢的区间
    i := l - 1
	// j不能遍历到r位置，因为r是中枢本身，查找完之后再做交换
    for j := l; j < r; j++ {
		// 遍历l到r，保证i左侧包括i位置记录的都小于等于x,右侧全部大于x
        if a[j] <= x {
            i++
            a[i], a[j] = a[j], a[i]
        }
    }
	// 最后遍历完交换r和i+1位置，把中枢放到正确的地方
    a[i+1], a[r] = a[r], a[i+1]
    return i + 1
}

• 维护左侧区间都比x小，所以初始化i为l-1
• 变量j遍历[l,r) 左闭右开区间，大于x无操作
• 小于x时候,i++，然后对调i和j位置的数字，这样又可以保证i左侧包括i位置的数都小于x
• 遍历结束以后i+1位置的数正好是最后一个比i大的数，把他和r对调
• 返回i+1，也就是中枢位置的下标

时间复杂度：运气好就是一次就找到了On运气不好每个数都找了一次ON^2，算法导论中把每次查找都使用一个随机数，可以显著提高效率，趋近于On，具体为什么可以自己去看

为什么推荐用快选，因为空间O1，时间On~On^2比堆的时间Onlogn和Ologk更快，但是快排也有局限性

• 快选需要修改原数组，如果原数组不能修改的话，还需要拷贝一份数组，空间复杂度就上去了。
• 堆只需要保存 k 个元素的小根堆。快速排序变形的方法如果不允许修改原数组那就要保存下来所有的数据，所以数据量大时用堆更好

引用： 优劣比较

代码： golang

15.三数之和 #

题目： 数组里有没有三个数加起来为0，找出所有可能的情况

题解：

• 先把数组排序
• 从小到大遍历这个数组，每次取一个元素，将这个元素的相反数设为target
• 在每次遍历中，使用双指针对当前元素的后面的所有元素进行处理，找到所有两个元素的和为target，这样，三个元素的和就是 0
• 双指针的具体处理方式为：头尾各一个指针，每次判断两个指针所指的元素的和与target的大小，如果和小了，左指针右移；如果和大了，右指针左移，直到两个指针相遇

注意：

• 因为不能有重复的结果，所以前后两次遍历取的元素如果相等，要采取跳过的操作
• 在第三步中，对当前元素的后面的所有元素进行处理的原因是，前面的元素已经找到了所有符合条件的可能，不需要再找

代码： golang 引用： 【LeetCode】15#三数之和

22.括号生成 #

题目： 数字n代表生成括号的对数,请生成所有可能的并且有效的 括号组合3

比如：

输入：n = 3
输出：["((()))","(()())","(())()","()(())","()()()"]

题解：

• 找不同可能性的题目，解题思路优先考虑深度优先dfs
• 既然是有效的括号组合而且只有小括号，那么只需要维护n个左括号，n个右括号的组合
• 深度优先，就是类似二叉树的遍历，使用模板

func dfs(根){
    dfs(左子)
    dfs(右子)
}

• 要维护左右括号的个数
• 因为是有效的括号，要先拼左括号再拼右括号，需要左右括号相等，所以

func dfs(左括号个数，右括号个数，当前字符串){
    if 左>右{
        return
    }
    if 左==右{
        append(res,当前字符串)
        return
    }
    if 左>0{
        dfs(左-1，右，当前+"(")
    }
    if 右>0{
        dfs(左，右-1，当前+")")
    }
}

注意：边界n==0不需要查找

代码： golang

103.二叉树的锯齿形层序遍历 #

题目： 先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进

题解：不改变原树结构，层遍历，维护正反bool条件，头插尾插，最终返回二维数组

代码： golang

39.组合总合 #

题目： 找出数组里所有和等于target的总合

题解：回溯，边界是sum大于target剪枝，等于就拿到一个结果

注意：append一维数组的时候要拷贝下

拷贝函数参考

var tmp []int
tmp = append(tmp,curr...)
res = append(res,tmp)

代码： golang

142. 环形链表 II #

题目： 找到交点坐标的下标，无环时返回null

题解：

• 这不仅仅是返回是否相交，还要找到交点的下标；我们知道可以用双指针相遇时说明相交
• 找到交点时，快指针正好比慢指针多一圈

设链表共有 a+b+c 个节点，链表头部到链表入口有 a 个节点（不计链表入口节点），相遇时快指针走了a+b+c+b次，慢指针走了a+b次，发件人指针是慢指针的两倍速度,可得

a+b+c+b = 2(a+b)
c=a

所以相遇时再加一个头指针一起跑，慢指针继续跑相遇点就是环的起始位置

代码不写了，比较简单

300.最长递增子序列 #

题目： 求最长递增子序列的长度，子序列是不连续的

题解：求最值，不用保存子序列，我们记录数组里每个数作为终点的序列最长长度就好了

• 对每个数都遍历之前的数，只要比当前数小，说明他可以作为终点
• 因为已经记录了之前数作为终点的序列长度，让序列长度+1就可以
• 再做下对比，公式如下

max(dp[i],dp[j]+1)

得到所有序列作为终点的最长子序列长度数组以后，遍历下取最值就好了

代码： golang

1143.最长公共子序列 #

题目： 求两个数组的最长公共子序列长度

题解：

• 用二维数组dp记录最长公共子序列长度，dp[i][j] 为当前位置最长公共子序列长度，状态转移方程

  // 其中因为当前字符相等，所以长度各减1的dp[i-1][j-1]表示没有当前字符时字符串的最长公共子序列长度
  // 也就是加入text1长度为i，text2长度为j，i j 就是当前长度的最长公共子序列,i-1 j 代表长度为i-1的字符串与j的字符串公共子序列长度
  if text1[i] == text2[j] then dp[i][j] = dp[i-1][j-1] + 1 
  // 长度不一样时对比各自长度-1，作为当前长度最长公共子序列
  if text1[i] != text2[j] then dp[i][j] = max(dp[i-1][j],dp[i][j-1])
  

注意：i-1 和 j-1 会越界，申明时让dp行列len+1

代码： golang

59.螺旋矩阵-ii #

题目： 给一个数字n，输出n*n的正方形螺旋矩阵

题解：生成一个 n×n 空矩阵 mat，随后模拟整个向内环绕的填入过程：

• 定义当前左右上下边界 l,r,t,b，初始值 num = 1，迭代终止值 tar = n * n；
• 当 num <= tar 时，始终按照 从左到右 从上到下 从右到左 从下到上 填入顺序循环，每次填入后：
  • 执行 num += 1：得到下一个需要填入的数字；
  • 更新边界：例如从左到右填完后，上边界 t += 1，相当于上边界向内缩 1。
• 使用num <= tar而不是l < r || t < b作为迭代条件，是为了解决当n为奇数时，矩阵中心数字无法在迭代过程中被填充的问题。

最终返回 mat 即可。

题解来源

代码： golang

搜索二维矩阵 #

题目： 递增的二维矩阵，搜索值是否在内部

题解：方法1，简单搜索

• 以二维数组左下角为原点，建立直角坐标轴。
• 若当前数字大于了查找数，查找往上移一位。
• 若当前数字小于了查找数，查找往右移一位。

题解来源

方法2，二分搜索（独创）

既然列递增，且行递增，下一行所有数字都比上一行大，可以把二维数组拼接起来，视为递增的一纬度数组来处理

• 取行列长度n1 n2，得到全局数字个数n1*n2
• 使用二分法，取数字时，mid/n2为行，mid%n2为列即可

我的题解

代码： golang

最后 #

如果文中有误，欢迎提pr或者issue，一旦合并或采纳作为贡献奖励可以联系我直接无门槛加入 技术交流群

我是小熊，关注我，知道更多不知道的技术